Conditional Maximum Loss Portfolio Optimization
This article summarizes the new Conditional Maximum Loss (CML) investment risk measure and presents an exclusive risk budgeting Python case study.
The Conditional Maximum Loss (CML) is a brand new investment risk measure introduced by Kristensen and Vorobets (2026).
CML is inspired by drawdowns but improves their practical and intuitive issues for portfolio optimization and risk budgeting.
CML is specifically designed for the next-generation investment framework, which is carefully presented in the Portfolio Construction and Risk Management book and studied in the Applied Quantitative Investment Management course.
Conditional Maximum Loss properties
CML is a natural generalization of CVaR in a multi-period setting.
Compared to drawdowns, which are measured against the high-water mark, CML is measured against the portfolio’s value at rebalancing times.
This aligns much more with how investment managers actually think about drawdowns in practice, and it allows us to solve the optimization problem in a fast and stable way, even for high-dimensional market simulations.
You can read much more about all the above in the article by Kristensen and Vorobets (2026), and you can find the article's accompanying Python code here.
Relation to CVaR
Conditional Value-at-Risk (CVaR) happens to be a lower bound for Conditional Maximum Loss (CML). Hence, the two risk measures are built on the same general principles and can therefore be optimized jointly, which you can see an example of in the case study from Kristensen and Vorobets (2026).
The main difference is that CML takes an average over the maximum loss over the entire path simulation, while CVaR is an average of the worst losses at the end of the horizon.
Hence, CML allows us to minimize the probability of hitting stop losses or experiencing client withdrawals as well as simply having a more positive path between portfolio rebalancing times.
Python case study
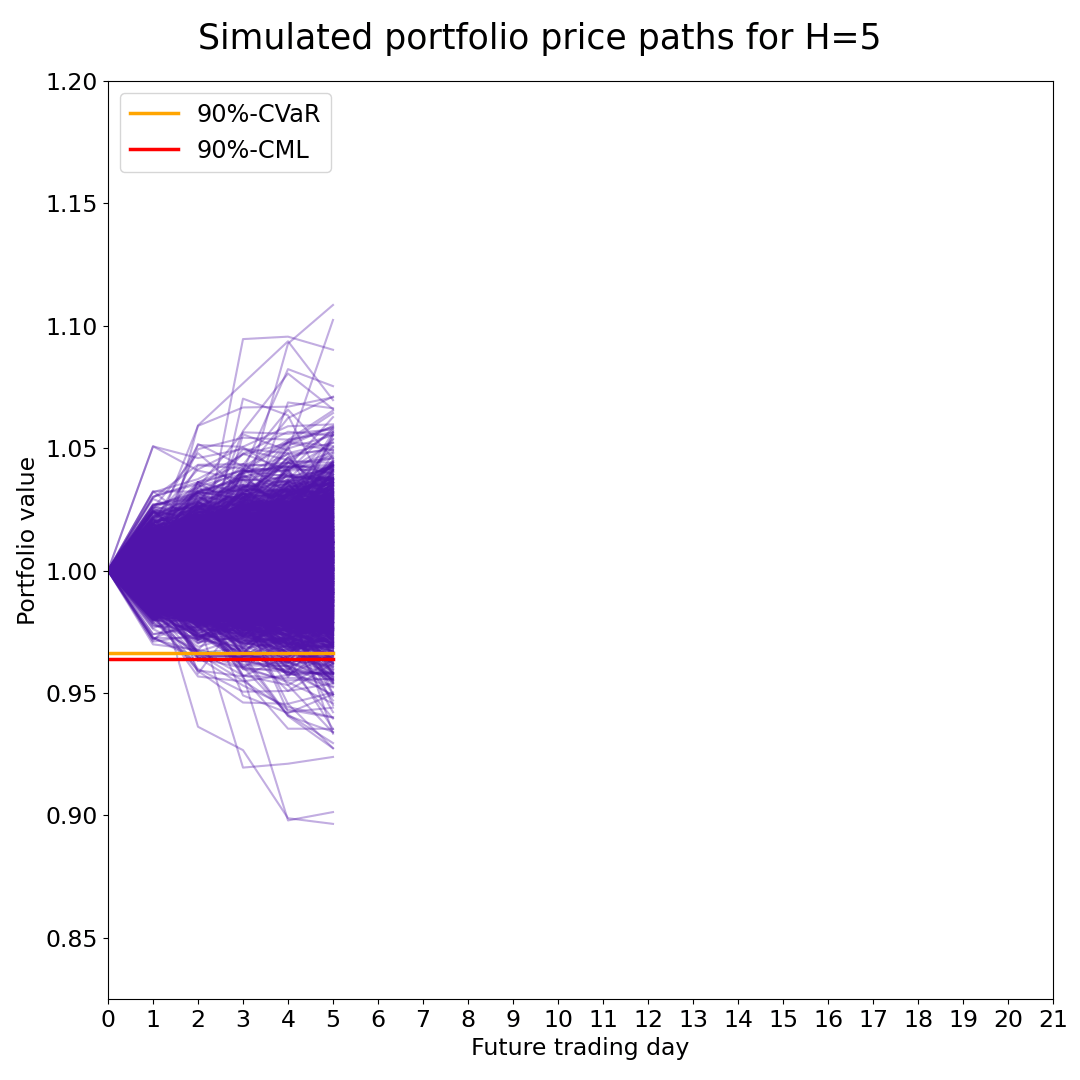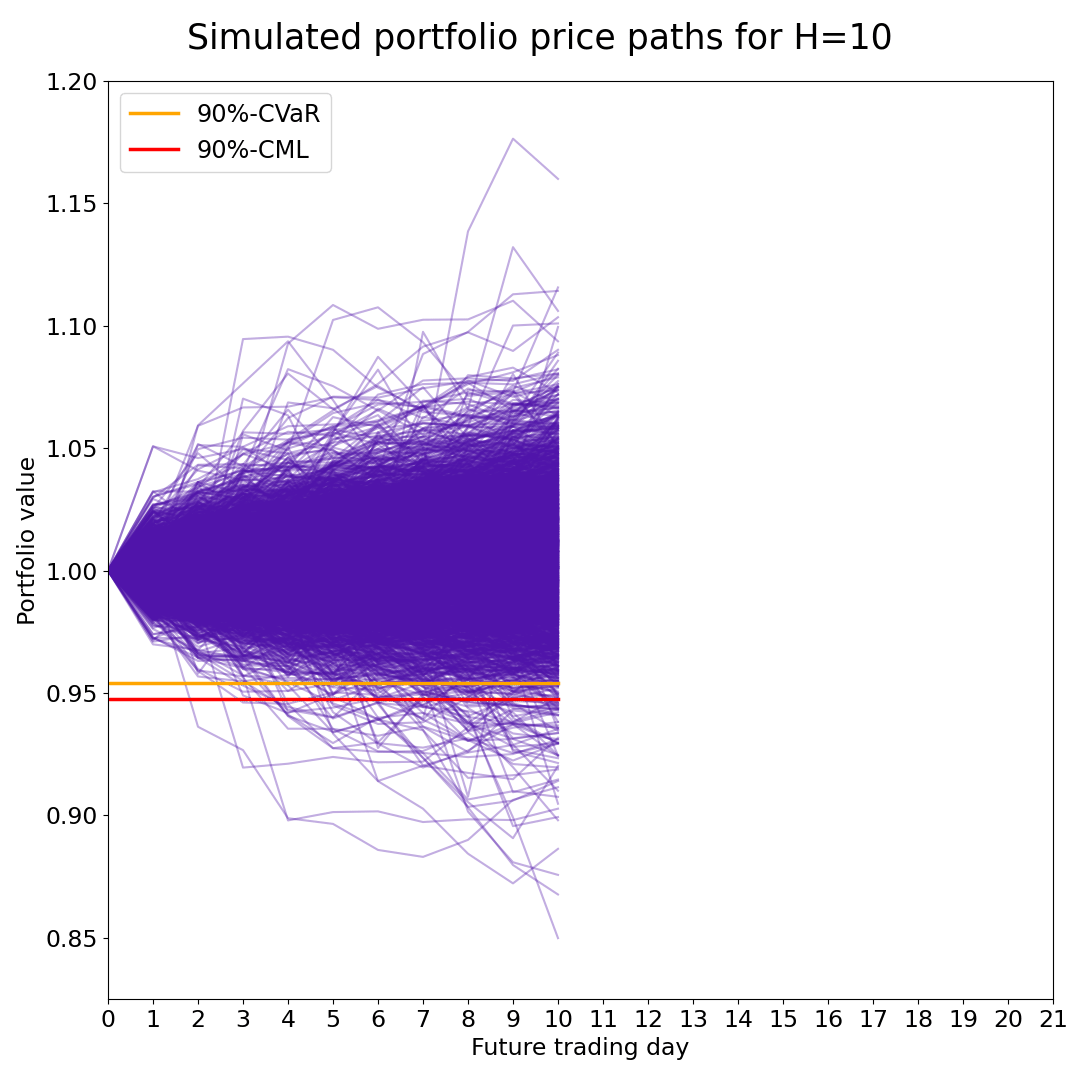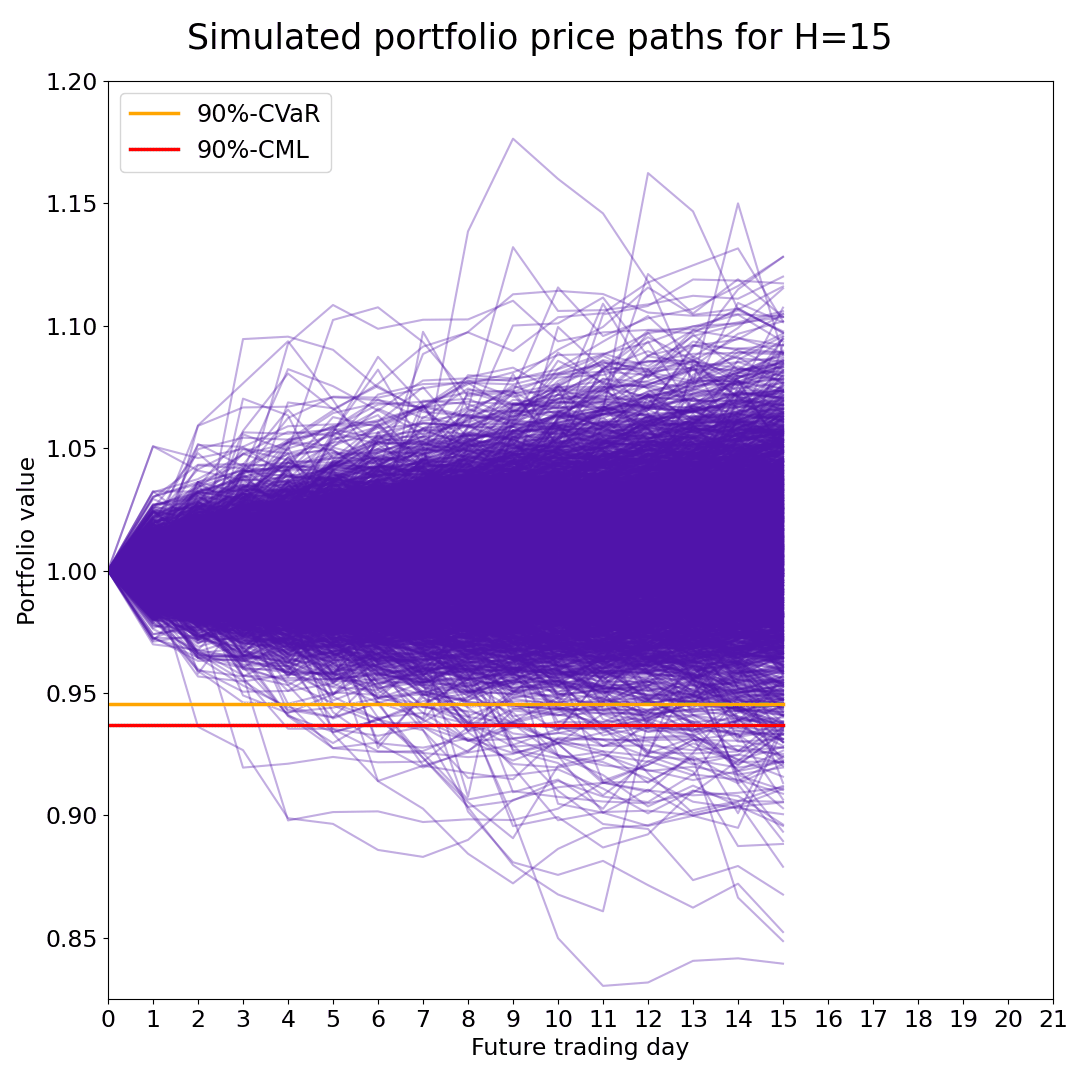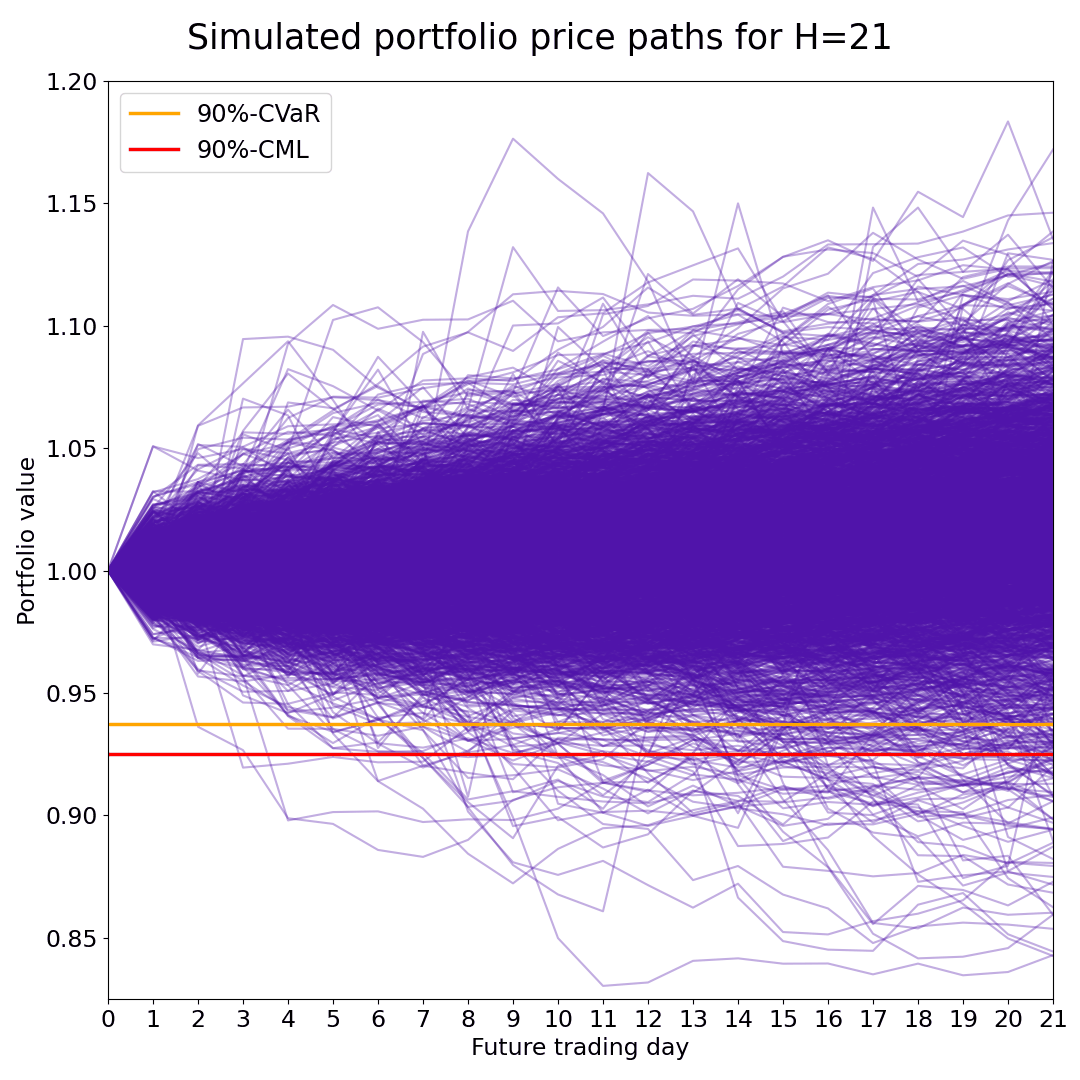
The case study for the article that introduces the Conditional Maximum Loss investment risk measure includes Python code, where we use the Fully Flexible Resampling method to simulate the P&L of 10 US equity indices 21 days into the future.
We then perform both CML and CVaR portfolio optimization with and without Sequential Entropy Pooling (SeqEP) views.
The article presents a simple linear programming algorithm for solving the CML and joint CML and CVaR portfolio optimization problems.
Risk budgeting case study
The exclusive Python case study below shows you how fast we can actually compute CML efficient portfolios, including CML tracking error risk budgets for advanced portfolio construction as explained in Section 6.3 of the Portfolio Construction and Risk Management book.
In the future, we will have several case studies that work with the CML investment risk measure for advanced investment analysis.
You can find all the exclusive case studies here. As a paid subscriber, you have full access to these case studies, the Applied Quantitative Investment Management course, and asking me questions from the Substack chat.