Derivatives Portfolio Management Framework

This post gives a high-level presentation of the Portfolio Management Framework for Derivative Instruments SSRN article.

Portfolio return distributions for CVaR and variance optimized multi-asset portfolios that include equity call and put options.

The Portfolio Management Framework for Derivative Instruments SSRN article¹ documents an elegant framework for handling derivative instruments in portfolio optimization and management.

Traditionally, in academia, the portfolio’s self-financing constraint is formulated as:

\(\sum_{i=1}^{I}w_{i}=1,\)

i.e., that the “portfolio weights must sum to one”.

While the traditional formulation works for simple cash-based portfolios, it is insufficient for more modern portfolios that include derivatives.

An unfortunate consequence of the academic formulation is that people usually attempt to introduce offsetting cash positions “to make everything sum to one” as a derivatives replicating strategy that imposes the self-financing constraint.

However, the offsetting cash approach is in fact unnecessarily complicated, because different cash positions need to be introduced to properly match the funding rates of the derivative instruments.

The replication argument also becomes invalid for slightly more exotic instruments such as variance swaps, where a cash exposure in the realized variance is not possible.

Performance evaluation usually becomes more complicated by the introduction of artificial cash positions that are not there in reality.

Luckily, it is possible and in fact much easier to simply treat the derivative instruments as they are, having an exposure e and a relative market value v.

With this separation, the exposures determine the portfolio’s future P&L distribution, while the market values are used for elementary bookkeeping.

Hence, a more general self-financing constraint that solves many practical issues is:

\(\sum_{i=1}^{I}v_{i}e_{i}=1.\)

As you can read in the article, the old self-financing constraint is a simple special case of the new. Hence, nothing is lost from using the more general formulation, while it helps us to elegantly handle derivatives.

Python case study

You can find a video walkthrough of the article and Python code in the video below:

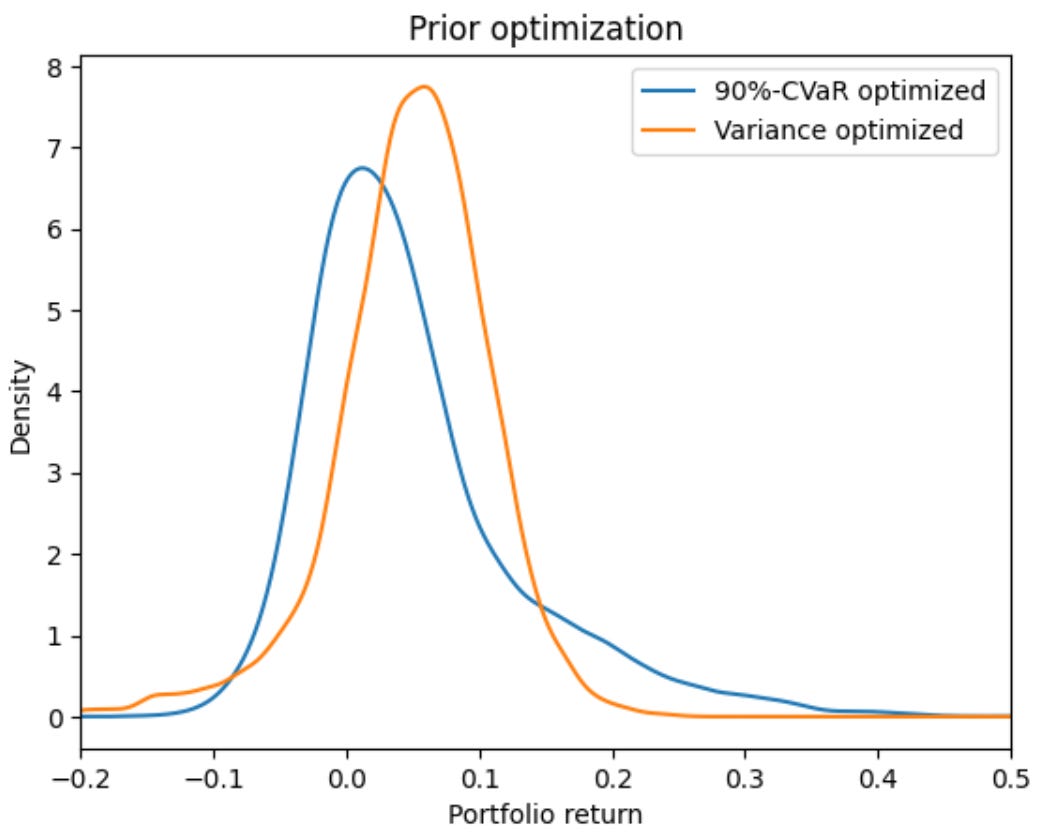
The accompanying code² to the article includes a Python case study where the framework is implemented to optimize the CVaR and variance of a multi-asset portfolio including six options written on the developed market equity index.

There is also an Entropy Pooling³ stress-test case study. For more sophisticated stress-testing and the best results, you should use Sequential Entropy Pooling⁴.

Exclusive case studies

Paid subscribers have access to an expanding collection of exclusive case studies going through the theory and methods presented above.

As a free subscriber, you can claim a one-time access to a paid post.

Consider a paid subscription to lock in the current subscription price.

1. Portfolio Management Framework for Derivative Instruments SSRN article: https://ssrn.com/abstract=4217884

2. Derivatives Framework Example Python code: https://github.com/fortitudo-tech/fortitudo.tech/blob/main/examples/5_DerivativesFramework.ipynb

3. Entropy Pooling Collection post: https://antonvorobets.substack.com/p/entropy-pooling-collection

4. Sequential Entropy Pooling post: https://antonvorobets.substack.com/p/sequential-entropy-pooling